流匹配：最优雅的损失函数

流匹配是近年来最流行的生成模型框架，因其优越的表现和简单的公式而闻名。这篇文章介绍了理解流匹配所需的基础知识，梳理了一条比较合理的思维路径，同时专注于最重要的公式。

流

在介绍流模型之前，我们已经看到了生成模型的发展线路：从单步直接生成（VAE、GAN）变成多步生成（Diffusion）。这种趋势表明，建模复杂的数据分布和简单的高斯分步之间的直接联系是困难的，而建模两者之间的分布会更容易些。Diffusion就是通过样本 $x_0$，创建了任意时间步 $t$ 的分布 $\mathcal{N}(x_t|\sqrt{\overline{\alpha}_t}x_0,(1-\overline{\alpha}_t)\mathbf{I})$ 。

除此之外，流模型也定义了源分布与目标分布的中间状态。流模型将时间定义在 $[0,1]$ 上，任意时刻的样本表示为：

$$x_t = \psi_t(x_0), \qquad t\in[0,1]$$

其中 $\psi_t$ 是随 $t$ 变化的函数，称作 Warping function。它被要求是一个双射，即不会在变换的过程中丢失信息。$x_0$ 则是从初始分布中采样的一个样本。

由于双射可逆，我们也可以将流模型变成一个马尔科夫链。首先有如下关系：

$$x_{t+\Delta t} =\psi_{t+\Delta t}(x_0), \qquad x_{t} =\psi_{t}(x_0),$$

那么很容易得到

$$x_{t+\Delta t} =\psi_{t+\Delta t}\circ\psi_{t}^{-1}(x_t) = \psi_{t+\Delta t|t}(x_t).$$

这种双射性质的好处在于可以精确的计算概率密度，而无需近似优化（例如VAE中的证据下界）。但双射的限制使得模型难以构建，我们很难找到现有的深度神经网络能够满足这一条件。而随着模型加深，概率似然也变得很难计算。这就引出了使用速度（Velocity）参数化 $\psi_t$ 的方法。

速度

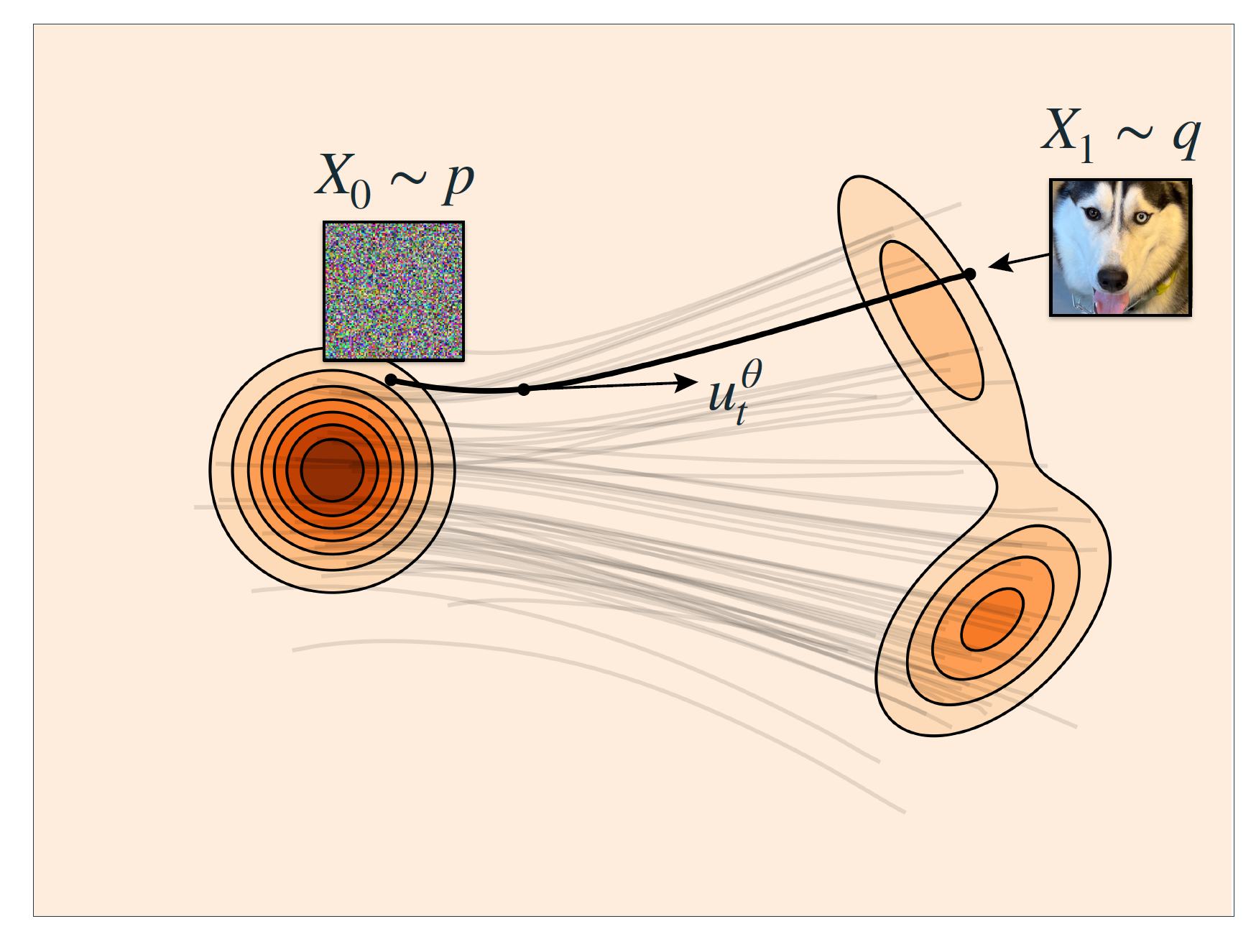
对于一个样本 $x_0$ ，我们能够创建一系列连样本 $x_{t_1}, x_{t_2},\cdots,x_1$ ，它们是连续变化的，因此 $x_t$ 是一个关于时间 $t$ 的函数。我们可以定义该函数在任意时刻的导数，也就是所谓速度：

$$\frac{\mathrm{d}}{\mathrm{d}t}x_t = u_t(x_t)$$

这是一个常微分方程。只要我们拥有速度，我们就无需关心 $\psi_t$ 到底是什么，只需要通过一步步的数值模拟去恢复即可，就像 Diffusion 做的那样。同时，这个过程本质也是在求解一个ODE，所以有可供使用的数值模拟方法。

训练目标

首先，我们并没有所谓速度的真值，它仍然需要定义，而定义它的关键在于 $x_t$ 本身。回想一下，我们的目标是从源分布中采样一系列数据点，然后计算每个点在每个时刻的速度，从而将它们推动到目标分布中。虽然我们提到过，这个变换是一个双射，所以存在一一对应关系。但是这种对应关系是无法预知的。这就抛出一个问题：

没有配对关系，还能构建概率路径吗？

答案是可以的。首先，我们的目标是找到 $t$ 时刻的分布 $p_t(x)$，那么根据全概率公式，可以将分布表示为条件分布的期望：

$$p_t(x)=\mathbb{E}_{y}p_t(x|y),$$

神经网络训练其实就是在优化期望，那么完全可以单独考虑 $p_t(x|y)$ ，也就是只考虑一个样本。发现了吗？我们已经有了“配对”关系。也就是说，谁和谁配对其实不重要，我们只需要全部采样一遍，然后优化平均值就行了。

有了上述认知之后，其实速度场也是一样的，直观上来说由于速度的线性性质，相加平均之后仍然是速度。因此我们只需要从目标分布中随机采样一个样本，然后计算路径的斜率。最简单的路径可以表示为匀速直线运动：

$$x_t = (1-t)x_0 + t x_1.$$

因此速度为

$$\frac{\mathrm{d}}{\mathrm{d}t}x_t=x_1-x_0 = u_t(x_t).$$

然后我们就导出了流匹配的优化目标：

$$L=\mathbb{E}_{t,x_0,x_1}\left\|u_t^{\theta}(x_t)-(x_1-x_0) \right\|^2.$$

这个损失函数被称为条件流匹配损失（CFM loss），如前所述，相对应的流匹配损失（FM loss）就是条件流匹配损失的期望，或者说：优化条件流匹配损失实现了对速度场的无偏估计。

上述结论的成立对损失函数的性质有要求，它必须是 Bregman 散度，而 MSE 是特殊的 Bregman 散度。这里不作展开。总之，我们需要一个目标样本，和一个适当的损失函数，仅此而已。

关于 $\psi_t(x|x_1)$

虽然 $\psi_t(x|x_1)=(1-t)x_0+tx_1$ 这种匀速运动方法看起来像是偷懒的结果，但它还真有一定的理论支撑。首先，在最优传输的定义中，我们需要最小化动能，也就是速度的平方：

$$E = \int_0^1 \mathbb{E}_{x_t\sim p_t}\|u_t(x_t)\|^2\mathrm{d}t,$$

这玩意没有解析解，但可以找到它的上界。我们先将速度写成路径的微分：

$$E = \int_0^1 \mathbb{E}_{x_t\sim p_t}\left\|\mathbb{E}\left[\dot{\psi}_t(x_0|x_1)\right]\right\|^2\mathrm{d}t,$$

其中 $\dot{\psi}_t(x_0|x_1)$ 表示给定目标样本 $x_1$ 时， $x_0$ 对应 $t$ 时刻速度。根据 Jenson 不等式放缩得到

$$E = \int_0^1 \mathbb{E}_{x_t\sim p_t}\left\|\mathbb{E}\left[\dot{\psi}_t(x_0|x_1)\right]\right\|^2\mathrm{d}t\le \int_0^1 \mathbb{E}_{x_0,x_1}\left\|\left[\dot{\psi}_t(x_0|x_1)\right]\right\|^2\mathrm{d}t$$

现在优化目标被转移到了单个目标上，正如我们之前做的那样。通过拉格朗日方程，可以知道加速度应当为0。那么在匀速运动的前提下，直线显然是最优解。但需要澄清的是，flow matching 没有真的构建最优传输，而是最小化了它的上界。如果真的是最优传输，理论上就不需要迭代了，完全可以一步生成。