PU-Net 论文阅读笔记

论文：PU-Net: Point Cloud Upsampling Network

一、摘要

由于数据的稀疏性和不规则性，使用深度网络学习和分析 3D 点云具有挑战性。论文提出了一种数据驱动的点云上采样技术，即 PU-Net ，其关键思想是学习每个点的多级特征，并通过多层卷积单元扩展特征，然后将这些特征重建为上采样点集。网络应用于 patch-level，通过联合损失函数驱使上采样点以均匀的方式分布在隐式表面上。最后论文通过一系列实验展现网络的效果，并阐述了其局限性。

二、相关工作

论文中将点云上采样的方法主要分为两类：基于优化（optimization-based）的方法和基于深度学习（deep-learning-based）的方法。

基于优化的方法

移动最小二乘法（Moving Least Squares, MLS）

参考论文：Computing and Rendering Point Set Surfaces

通过已有点的局部信息估计平滑表面，并将其投影到表面上，可以实现点云的平滑，同时因为描述了表面结构，可以实现上采样和下采样。假设从表面 $S$ 上获取到点 $p_i \in \mathbb{R}^3,i\in \{1,2,\dots,N \}$ ，目标是将 $S$ 附近的点 $r$ 投影到近似表达 $p_i$ 的二维表面 $S_P$ 上。

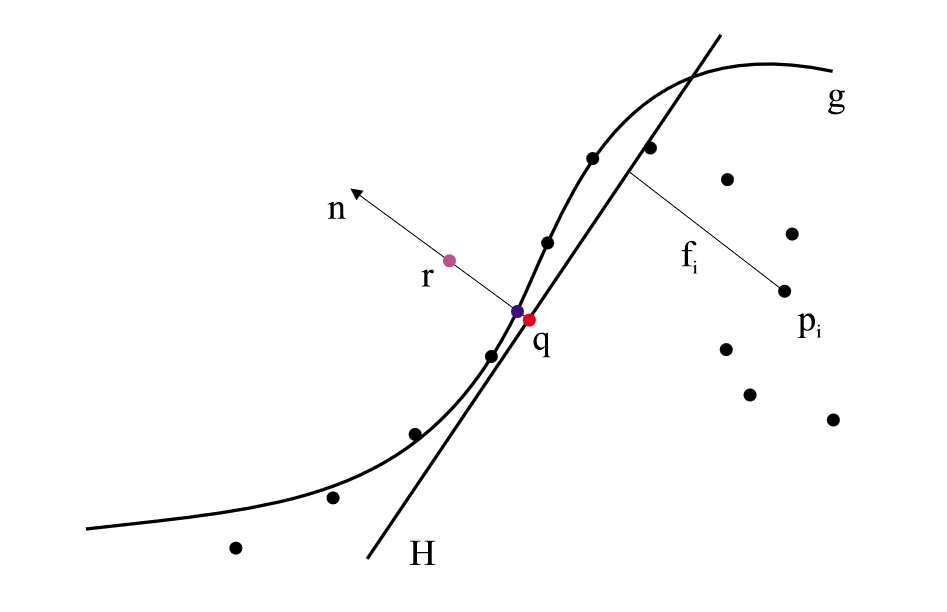
首先找到 $r$ 的局部参考域（Local Reference Domain） $H$ ，$H$ 是一个平面，可以通过其单位法向量 $n$ 以及原点到平面的距离 $D$ 共同定义，即 $H = \{x|\left< n,x \right> - D = 0,x\in\mathbb{R}^3 \}$ 。参考域 $H$ 通过最小化加权距离平方和得到：

$$\sum_{i=1}^{N}(\left< n,p_i \right>-D)^2\theta\left(\| p_i - q \|\right)$$

其中 $\theta$ 是一个平滑的单调递减函数，在整个空间上都是正的，如 $\theta(d)=e^{\frac{d^2}{h^2}}$ 。考虑到点到平面距离同样可以转换到 $q$ 点上：$(\left< n,p_i \right>-D)^2 = (\left< n,p_i-q \right>)^2$ ，将 $q$ 点坐标写作 $r+tn$ ，则式子改写为：

$$\sum_{i=1}^{N}(\left< n,p_i-r-tn \right>)^2\theta\left(\| p_i - r-tn \|\right)$$

函数的因变量为 $t$ 和 $n$ ，可以通过非线性最小二乘的方式求得。

然后计算局部图（Local Map），即通过多项式近似来拟合曲面。如上图所示，令 $f_i$ 为 $p_i$ 到 $H$ 的距离，即 $f_i= n \cdot (p_i-q)$ 。设多项式函数为 $g$ ，则其系数通过最小化下式得到：

$$\sum_{i=1}^{N}(g(x_i.y_i)-f_i)^2\theta(\| p_i - q \|)$$

这里 $(x_i,y_i)$ 是 $p_i$ 点投影到 $H$ 平面的坐标， $q$ 为原点。总而言之，从 $H$ 的视角来看，其它点分布在其上下，利用多项式拟合了一个凹凸不平的曲面 $S_P$ 来接近所有点，其中离原点 $q$ 越远的点权重越低。

最后进行投影操作。$r$ 点的投影即为为原 $g,\mathrm{g}$ 点处的多项式值，即：

$$\mathscr{P}(r)=q + g(0,0)n = r+(t+g(0,0))n$$

该算法涉及到两次最小二乘，其中第一次的相对复杂一些，可能需要一些假设或技巧来求解，这里不展开。

局部最佳投影（Local Optimal Projection, LOP）

参考论文：Parameterization-free Projection for Geometry Reconstruction

MLS 方法假设局部平面可以很好地近似局部几何形状，并不能适用于复杂形状。因此设计一个新的不使用局部方向信息（参考平面或法线）的算子来解决这一问题，也就是 LOP 算子。

问题仍然是一个投影问题：给定数据点集 $P = \{p_j\}_{j\in J}\subset \mathbb{R}^3$ ，将任意点集 $X^{(0)}=\{x^{(0)}_i\}_{i\in I}\subset \mathbb{R}^3$ 投影到 $P$ 上，投影点集为 $Q = \{q_i\}_{i\in I}$ 。

为了使投影后点逼近 $P$ 的几何形状，且考虑到距离越远的点作用越弱，定义代价函数 $E_1$ 表达式为：

$$E_1(X,P,Q)=\sum_{i\in I}\sum_{j\in J}\|x_i-p_j\|\theta(\|q_i-p_j\|)$$

同时为了避免投影后点太靠近彼此，定义代价函数 $E_2$ 表达式为：

$$E_2(X,Q)=\sum_{i'\in I}\lambda_{i'}\sum_{i\in I \setminus \{i'\}}\eta(\|x_{i'}-q_i \|)\theta(\|q_{i'}-q_i \|)$$

其中 $\eta(r)$ 同样是一个递减函数，对彼此接近的 $q_{i}$ 进行惩罚，使得投影后分布均匀。通常为 $\eta(r)=1/3r^3$ 。 $\{\lambda_i\}_{i\in I}$ 是一个平衡项，用 $\Lambda$ 表示。若 $\Lambda$ 较大，则以形状不近似的代价去追求分布均匀；若 $\Lambda$ 较小，则以分布不均的代价去追求形状近似。论文在后续对参数的选取做了比较复杂的证明，但实在是看不懂。

小结

MLS 和 LOP 是较为常用的基于优化的方法，但它们假设物体表面为光滑流形，对边缘的还原较差。也有基于边缘感知的方法，但依赖于好的参数；总的来说，基于优化的方法都不是数据驱动的，严重依赖先验知识。

基于深度学习的方法

论文：此前没有专注于点云上采样的神经网络。

三、网络架构

局部区域生成（Patch Extraction）

考虑到上采样需要利用物体的局部几何信息，论文采用了 patch-based 的方式，也就是从物体点云中收集各种形状的局部区域来训练网络。

具体来说，首先从物体表面随机选取 $M$ 个点，并从每个选择的点开始，沿着表面生长出一个 patch 。并规定在每个 patch 内，任意两点之间的测地线距离小于一定的阈值 $d$ 。随后，论文使用[泊松盘采样](# 泊松盘采样)（Poisson-disk Sampling），从每个 patch 上随机生成 $\hat{N}$ 个点作为该 patch 上参考基准（ground truth）点。同时为了利用到局部和全局信息，论文通过改变 $d$ 的大小来提取不同比例和密度的 patch 。

泊松盘采样

泊松盘采样的目的是从原始点中采样一部分点，使得任意两点间距离都不会太近。泊松盘采样可以用于随机生成一组分布均匀的点，也可以从已有的点中进行采样。下面主要介绍后者的方法。

1. 初始化参考点列表：在每个 patch 上初始化一个参考点列表，这个列表最开始为空；
2. 选择第一个参考点：在每个 patch 上随机选择一个点作为第一个参考点，并将其添加到参考点列表中；
3. 生成新参考点：在距离第一个参考点一定距离范围内，随机生成一个新的参考点，并将其添加到参考点列表中。这个距离范围通常由两个参数决定，一个是最小距离 $r$ ，表示新生成的点与已有参考点之间的最小距离；另一个是采样次数 $k$ ，表示在一个点附近最多采样 $k$ 个点。
4. 验证新参考点：为了避免新参考点太接近已有的参考点，需要对新生成的参考点进行验证。如果新参考点与其他参考点之间的距离都大于等于 $r$ ，则接受新参考点，并继续进行步骤 3 。否则，舍弃新参考点，重新生成一个新的参考点，并重复步骤 4 ，直到找到符合条件的新参考点。
5. 重复步骤 3 和 4 ，直到达到预设的参考点数量或者无法再添加新的参考点为止。

泊松盘采样算法是一个计算密集型的过程，因此需要采用高效的算法来实现。通常，可以使用基于网格的算法（例如网格边长为 $r$ ，则非相邻的网格内两点距离一定大于 $r$ ）或基于随机抽样的算法来实现泊松盘采样。

点特征嵌入（Point Feature Embedding）

为了从 patch 中学习局部和全局几何上下文，考虑以下两种特征学习策略，它们的优点相互补充。

分层特征学习

论文采用了 PointNet++ 中提出的层级特征学习机制作为网络的最前端，从而在不同尺度上提取点云的局部和全局特征。同时因为点云上采样需要涉及到更多的局部上下文，特地在每个级别中使用了相对较小的分组半径（grouping radius）。关于分层特征学习以及 PointNet++ 相关内容，参考笔记 PointNet 和PointNet++ 。

多级特征聚合

网络中较低层对应较小尺度的局部特征，较高层对应较大尺度的局部特征。在 pointnet++ 中采用了 skip link 来联合多级特征，但论文在实验中发现“这种自上而下的传播”方法不适合上采样问题（但似乎没有给出具体原因）。因此论文给出的方法是直接组合来自不同级别的特征，并让网络学习每个级别的重要性。

如下图的 Point Feature Embedding 部分，补丁的输入为大小 $(N,3)$ 的坐标矩阵，在分层特征提取的过程中不断被下采样，同时特征被提取为不同的尺寸。为了融合不同特征，将每一层的特征上采样（反距离加权插值）为行数为 $N$ 的特征矩阵，并利用 $1\times 1$ 卷积将特征长度减少为 $C$ ，最后直接拼接起来得到嵌入点特征 $f$ 。

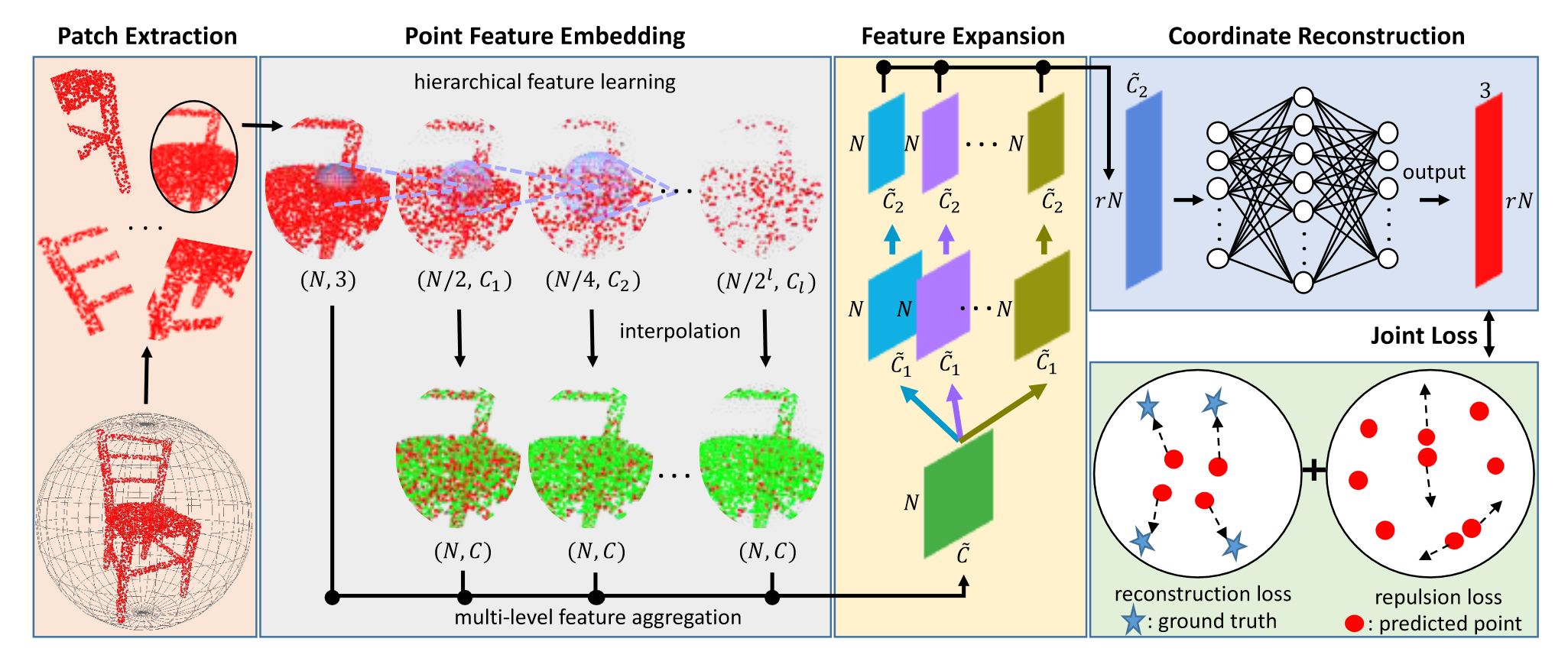
特征扩展（Feature Expansion）

在点特征嵌入组件之后，论文扩展了特征空间中的特征数量，从而扩大了点的数量，达到上采样的目的。假设 $f$ 的维度为 $N\times \widetilde{C}$ ，$N$为输入点数， $\widetilde{C}$ 为嵌入特征的特征维度。特征扩展操作将输出维度为 $rN \times \widetilde{C}_2$ 的特征 $f'$，其中 $r$ 是上采样率，$\widetilde{C}_2$ 是新的特征维度。本质上，这类似于图像相关任务中的特征上采样，在图像中可以通过反卷积（也称为转置卷积）或插值来完成。然而，由于点的不规则性和无序性，将这些操作应用于点云并非易事。因此，论文提出了一种基于亚像素卷积层的有效特征扩展操作。该操作可以表示为：

$$f'=\mathcal{RS}(\ [\ \mathcal{C}^2_1(\mathcal{C}^1_1(f)),\dots,\mathcal{C}^2_r(\mathcal{C}^1_r(f))\ ]\ )$$

其中 $\mathcal{C}_{i}^1$ 和 $\mathcal{C}_{i}^2$ 是两个独立的 $1\times1$ 卷积，$\mathcal{RS}$ 是一个 reshape 操作，将大小为 $N\times r\widetilde{C}_2$ 的张量转换成大小为 $rN\times\widetilde{C}_2$ 的张量（以此实现点数的放大）。

论文提到，嵌入特征 $f$ 已经聚合了来自邻域点的相关信息，因此在特征扩展时无需明确考虑空间信息。同时为了让扩张的特征相关性降低（避免生成的点距离太近），因此在 $\mathcal{C}_{i}^1$ 的基础上添加了 $\mathcal{C}_{i}^2$ 。这种特征扩展可以通过对 $r$ 个特征集应用分离卷积实现（如上图所示），也可以通过计算效率更高的分组卷积来实现。

关于分组卷积的概念，参考了飞浆的文档 。简单来说，普通卷积有 $C_2$ 个，尺寸为 $h_1\times w_1\times C_1$ ，将大小为 $H_1\times W_1\times C_1$ 的输入张量转换为大小为 $H_2\times W_2\times C_2$ 的输出张量。分组卷积则将原始输入张量分割为 $g$ 个大小为 $H_1\times W_1\times \frac{C_1}{g}$ 的张量，对应地，将卷积核尺寸变为 $h_1\times w_1\times \frac{C_1}{g}$ ，卷积个数变为 $\frac{C_2}{g}$ ，使得输出尺寸为 $H_2\times W_2\times \frac{C_2}{g}$ 。最后将 $g$ 个输出拼接即可。如下图所示：

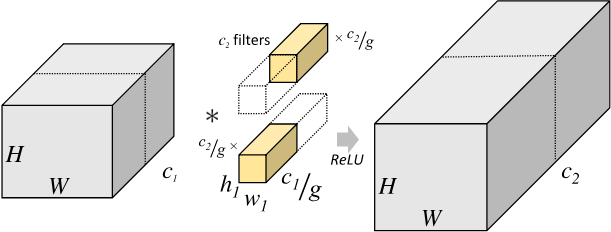
普通卷积的参数量为 $h_1\times w_1 \times C_1\times C_2$ ，而分组卷积的参数量缩减为：

$$h_1\times w_1\times \frac{C_1}{g} \times \frac{C_2}{g}\times g=h_1\times w_1 \times C_1\times C_2\times\frac{1}{g}$$

针对特征扩展问题，则将 $\widetilde{C}$ 视作通道数目，将其进行分组从而实现加速。

坐标重建（Coordinate Reconstruction）

得到 $rN\times\widetilde{C}_2$ 的张量后，将其重建为坐标值。论文采用了一系列全连接层来对每个点的特征回归 3D 坐标，最终输出 $rN\times3$ 的上采样坐标。

四、端到端训练

训练数据生成

对于一个稀疏的输入点云，实际上有许多可行的输出点分布。因此论文采用了在每个训练时期以 $r$ 的下采样率从 ground truth 点集中随机采样的方法，生成一些列输入点集，从而为给定的稀疏输入点分布模拟出来许多可行的输出点分布（不应该是输入点分布么？）。同时该方法可以进一步扩大训练数据集。

联合损失函数

为了鼓励生成的点以更均匀的方式分布在底层对象表面上，论文提出了结合重建损失（Reconstruction Loss）和排斥损失（Repulsion Loss）的联合损失函数。

重建损失函数

对于两组点云之间的距离度量方法，主要有 CD（Chamfer Distance）和 EMD（Earth Mover’s Distance），下面分别做详细介绍，主要参考 A Point Set Generation Network for 3D Object Reconstruction from a Single Image 这篇文章。

EMD

EMD 也称作“推土机距离”，通过定义“工作量”——即将一个分布搬运到和令一个分布相同所需的搬运量和搬运距离乘积总合——来衡量两组分布之间的相似性。数据的分布经常用直方图来表示，而对于点云，这个定义会简洁一些，目标是找到预测点云 $S_P\subseteq \mathbb{R}^3$ 和参考基准点 $S_{gt}\subseteq \mathbb{R}^3$ 之间的一个双向映射 $\phi$（既是单射又是满射，也就是一一对应的映射），使每个点与其映射的点之间的距离总和最小，也就是“搬运”的工作量最小即可：

$$L_{rec} = d_{EMD}(S_p,S_{gt})=\underset{\phi:S_p\rightarrow S_{gt}}{\min}\sum_{x_i\in S_p}\|x_i-\phi(x_i) \|_2$$

虽然概念上简单，但是 EMD 是一个优化问题，运算量比较大，可以通过给每个点分配固定的时间量并在一定错误率内终止来加快运行速度。

CD

CD 也称作“倒角距离”，定义为最近距离的平方和：

$$d_{CD}(S_1,S_2)=\sum_{x\in S_1}\underset{y\in S_2}{\min}\|x-y\|^2_2+\sum_{y\in S_2}\underset{x\in S_1}{\min}\|y-x\|^2_2$$

“由于三角不等式不成立，严格意义上 $d_{CD}$ 并非距离函数”。关于文章中提到的这点，反例很容易举出。在网上博客大多会找到这样的版本：

$$d_{CD}(S_1,S_2)=\frac{1}{\|S_1\|}\sum_{x\in S_1}\underset{y\in S_2}{\min}\|x-y\|^2_2+\frac{1}{\|S_2\|}\sum_{y\in S_2}\underset{x\in S_1}{\min}\|y-x\|^2_2$$

这个式子进一步考虑了两个点云数量不同的情况。

除了上述两种度量方式，还有此前在 PCL 笔记里记过的 Hausdorff 距离（点到点集的最小距离的最大值），但显然不太适用于这里。

方法对比

文章中用两种损失函数来计算一系列“平均形状”，从而对两者进行对比分析，如下图所示。

平均形状的具体计算方法没有详细说明，只提到用随机梯度下降法来最小化距离函数。从结果来看，平均形状的点数应该是固定好的，并且有一个合适的初始位置。

观察图中的平均形状，论文给出了以下结论：

1. 在第一种和第二种情况下，只有一个连续变化的隐藏变量，即 (a) 中的圆半径和 (b) 中的弧段位置。EMD 粗略地捕获了对应于隐藏变量的平均值的形状。相比之下，CD 会产生一种模糊形状，其几何结构呈飞溅形状；
2. 在后两种情况下，存在分类隐藏变量：正方形位于 © 的哪个角以及在条形 (d) 旁边是否有圆。CD 将少量的点分布在主体之外的正确位置；而 EMD 则严重扭曲了主体之外的点。

总的来说，EMD 对主体形状的拟合能力更强，而 CD 对总体形状的保持能力更强。论文中采用了 EMD 。

排斥损失（Repulsion Loss）

为了生成更加均匀分布的点，论文设计了排斥损失，表达式为：

$$L_{rep}=\sum_{i=1}^{\hat{N}}\sum_{i'\in K(i)}\eta(\|x_{i'}-x_{i} \|)w(\|x_{i'}-x_{i} \|)$$

其中 $\hat{N}=rN$ ，是输出点的数量；$K(i)$ 是点 $x_i$ 的 $k$ 近邻点的索引集合；$\eta$ 称为排斥项，是一个递减函数，用于在两个点距离太近时对其惩罚；$w(r)=e^{-r^2/h^2}$ ，用于使惩罚项随距离快速衰减。这个表达式以及函数形式的选择参考了[局部最佳投影（LOP）](#局部最佳投影（Local Optimal Projection, LOP）) 。

联合函数

最终得到联合损失函数如下式，其中 $\theta$ 表示网络中的参数，$\alpha$ 用于平衡重建损失和排斥损失，而 $\beta$ 表示权重的 $L_2$ 正则化项的乘数，用于降低模型参数值以防止过拟合。

$$L(\theta)=L_{rec}+\alpha L_{rep}+\beta\|\theta\|^2$$

五、实验

现在还没跑过实验，先看看论文里咋做的。

数据集

由于点云上采样没有公共基准，我们从 Visionair 存储库中收集了 $60$ 个不同模型的数据集，范围从光滑的非刚性物体（例如 Bunny）到陡峭的刚性物体（例如 Chair）。其中，我们随机抽取 $40$ 个进行训练，其余的用于 testing 。我们为每个训练对象裁剪 $100$ 个补丁，总共使用 $M = 4000$ 个补丁来训练网络。对于测试对象，我们使用蒙特卡洛随机采样方法在每个对象上采样 $5000$ 个点作为输入。为了进一步证明我们网络的泛化能力，我们直接在 SHREC15 数据集上测试我们训练有素的网络，该数据集包含来自 $50$ 个类别的 1200 个形状。具体来说，我们从每个类别中随机选择一个模型进行测试，考虑到每个类别包含 $24$ 个不同姿势的相似对象。至于 ModelNet40 和 ShapeNet ，我们发现由于网格质量低（例如，孔洞、自相交等），很难从这些对象中提取补丁。因此，我们使用它们进行测试；结果见补充材料。

实施细节

每个补丁的默认点数 $\hat{N}$ 为 $4096$，上采样率 $r$ 为 $4$。因此，每个输入补丁有 $1024$ 个点。为了避免过度拟合，我们通过随机旋转、移动和缩放数据来扩充数据。我们在点特征嵌入组件的四个级别中分别使用分组半径 $0.05、0.1、0.2$ 和 $0.3$ ，恢复特征的维数 $C$ 为 $64$。排斥损失中的参数 $k$ 和 $h$ 分别设置为 $5$ 和 $0.03$ 。平衡权重 $α$ 和 $β$ 分别设置为 $0.01$ 和 $10^{−5}$ 。实现基于 TensorFlow。为了优化，我们使用 Adam 算法训练网络 $120$ 个 epoch，mini-batch size 为 $28$ ，学习率为 $0.001$ 。训练在 NVIDIA TITAN Xp GPU 上花费了大约 $4.5$ 小时。

评估指标

为了定量评估输出点集的质量，我们制定了两个指标来衡量输出点与地面真值网格之间的偏差，以及输出点的分布均匀性。

对于表面偏差，我们为每个预测点 $x_i$ 在网格上找到最近的点 $x_i$ ，并计算它们之间的距离。然后我们计算所有点的均值和标准差作为我们的指标之一。

对于均匀性指标，我们在物体表面随机放置 $D$ 个大小相等的圆盘（在我们的实验中 $D = 9000$）并计算圆盘内点数的标准差。我们进一步归一化每个对象的密度，然后计算测试数据集中所有对象的点集的整体均匀性。因此，我们将磁盘面积百分比 $p$ 的归一化均匀系数 (NUC) 定义为：

$$\begin{aligned} avg &= \frac{1}{K*D}\sum_{k=1}^K\sum_{i=1}^D\frac{n_i^k}{N^k*p}, \\ NUC &= \sqrt{\frac{1}{K*D}\sum_{k=1}^K\sum_{i=1}^D\left(\frac{n_i^k}{N^k*p}-avg\right)^2}, \end{aligned}$$

其中 $n_i^k$ 是第 $k$ 个物体在第 $i$ 个圆盘内的点数，$N^k$ 是第 $k$ 个物体上的总点数，$K$ 是测试物体的总数，$p$ 是圆盘面积占总物体表面积的百分比。$n_i^k/(N^k*p)$ 在均匀分布的理想前提下为 $1$ ，$avg$ 表示该值的平均值。$NUC$ 相当于表达了该值的方差。需要注意的是，我们使用测地距离而不是欧几里得距离来形成圆盘（用测地线距离怎么形成大小相等的圆盘？）。

性能对比

尽管 PU-Net 是第一个专门用于上采样的网络，但还是找了 PointNet 和 PointNet++ 以及 PointNet++（MSG）来作对比，具体方法则是用它们的分割模块来做特征嵌入，然后用重建损失函数训练。但是最后给出的对比表格是用于评价均匀性的 NUC 指标？这是不是不太公平哈哈。剩下的对比和实验就不记录了，大致就是在不同的数据集上测试了一下效果。

五、总结

PU-Net 主要的内容概括如下：

• 在局部区域生成方面，采用了泊松盘采样，提供了均匀性和随机性；
• 在特征嵌入方面，参考了 PointNet++ 中的分层学习，并且采取了更直接的组合方式；
• 在特征扩展方面，利用 $1\times1$ 卷积对特征上采样，并重组为 $rN\times \widetilde{C}_2$ 的矩阵；最后对该矩阵进行特征重组，直接得到点坐标；
• 采用了联合损失函数，包括重建损失（EMD）、排斥损失（参考 LOP 方法）以及参数正则化项；
• 通过 NUC 指标评价生成点的均匀性。

关于网络的局限性，论文提到了两方面：

• 网络不是为补全而设计的，因此不能填补大洞和缺失的部分；
• 网络无法为严重欠采样的微小结构添加有意义的点。

同时也指出可以研究更多下采样方法，来生成更多的不规则稀疏数据用于训练。